Après vous avoir proposé un logiciel facilitant la réalisation des mathématiques au lycée, je vous propose d’aller vers le concret et de voir comment les lycéens utilisant un ordinateur peuvent faire rapidement un exercice, ici, sur les fonctions.
Comme cette page contient un grand nombre d’images, il est possible que son affichage soit un peu ralenti. Si c’est le cas, soyez patients !
Calcul de dérivée (Géogébra)
Résoudre une équation (Géogébra)
Tracer une courbe dans un intervalle (Géogébra)
Réaliser une lecture graphique (Géogébra)
Calculer l’image d’un nombre (Géogébra)
Réaliser un tableau de signes (PdfAdd)
Réaliser un tableau de variations (PdfAdd)
Attention : sous Géogébra, tu peux vérifier tes calculs mais donner le résultat n’est pas suffisant. Au bac, on te demande de montrer que tu es capable de démontrer le résultat que tu trouves.
Voici l’énoncé

Alors comment faire lorsqu’on est à l’ordinateur ?
1°) Calculer f’(x) et étudier son signe
J’ouvre Géogébra et je rentre dans ma barre de saisie ma fonction
| Barre de saisie : f(x)=(x²+4x+2)/(2(x+2) |
Pour réaliser un exposant sous Géogébra, tu peux :
- Utiliser le signe ^ par exemple x^2 pour x²
- Utiliser la touche « Alt » par exemple x(alt et en même temps 3) = x3
Ma courbe s’affiche alors.

Calculer f’(x)
Faire son calcul normalement.
Vérifier sous Géogébra
Sous Géogébra
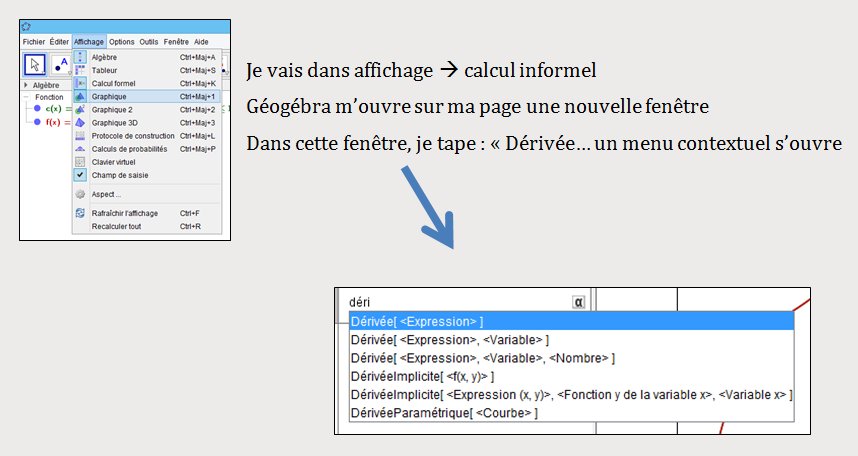
Je sélectionne Dérivée [ <expression>]
Je replace expression par ma fonction (ici dans mon exemple f(x))
Donc dans :
Calcul formel : Dérivée [ <expression>] |

Géogébra m’a donc donné la dérivée de f(x).
Le f’(x) donné par Géogébra est trop complexe pour réaliser mon étude de signes.
Je vais lui demander de développer l’expression.
Je tape « Développer[ <Expression> ». Généralement, quand tu commences à taper, le menu déroulant s’ouvre et il te suffit de choisir la bonne expression.
Attention aux accents !
<Expression> est sélectionné pour que tu rentres sa valeur. Il te suffit alors de cliquer sur la réponse donnée par Géogébra pour la dérivée.
Calcul informel : Développer[ <Expression> ] |

Étude du signe
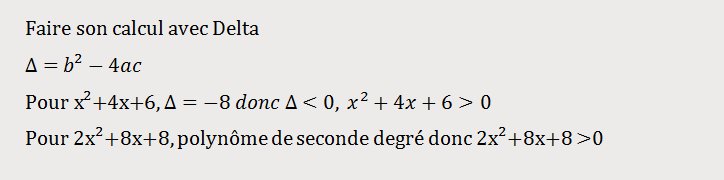

Je clique sur « Aperçu »

Rogner l’image (Si on ne sait pas rogner une image sous Word, voir ici.)

2°) Dresser le tableau de variation de f(x)
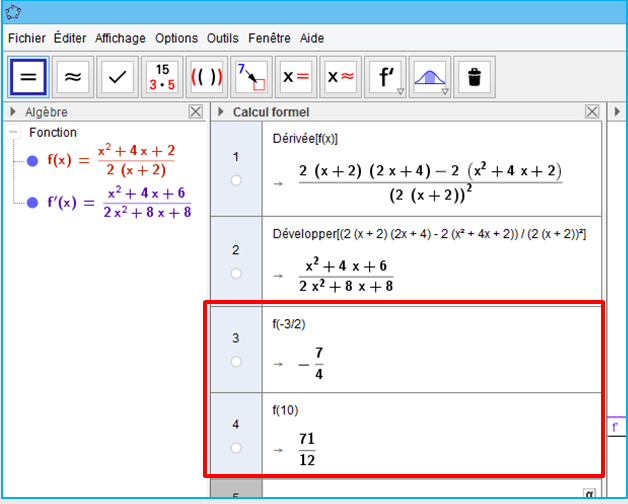
Je calcule f(-3/2) et f(10)
Calcul formel sous Géogébra
Je fais mon tableau de variations
Je complète le tableau réalisé sous PddAdd

Puis aperçu + rogner

3°) Déterminer les coordonnées du point d’intersection de la courbe (C) et de l’axe des abscisses.
Je dois calculer f(x) = 0
Donc calcul de Delta et de x1 et x2
Je vais donc résoudre cette équation avec l’aide de Géogébra
Dans Calcul formel : Résoudre[ <Équation en x> ] |
Ici dans l’exemple : Résoudre[ f(x)=0 ]

Si je veux un résultat arrondi, je clique sur l’icône ≈

Si je veux un arrondi particulier, je vais dans Options/Arrondi


4°) Tracer la courbe
Pour tracer une courbe dans un intervalle sur Géogébra, j’utilise la commande suivante
Barre de saisie : Fonction[ <Fonction>, <de>, <à> ] |
Fonction[f(x)=(x^2+4x+2)/(2(x+2), -3/2 , 10 ]

5°) Donner l’équation de la tangente T à la courbe (C) au point d’abscisse 0 et tracer cette tangente sur le dessin précédent.
Je calcule l’équation de la tangente
Tangente T au point d’abscisse 0 a pour équation : y = f’(0)(x-0) + f(0)
Sous Géogébra, je calcule f’(0) et f(0)


Je trace la tangente
Je trace T avec Géogébra
6°) Tracer sur le dessin précédent la courbe représentative de la fonction x → 1/x – Déterminer graphiquement le nombre de solution de l’équation f(x) = 1/x et en donner des valeurs approchées.
Je trace la courbe avec Géogébra
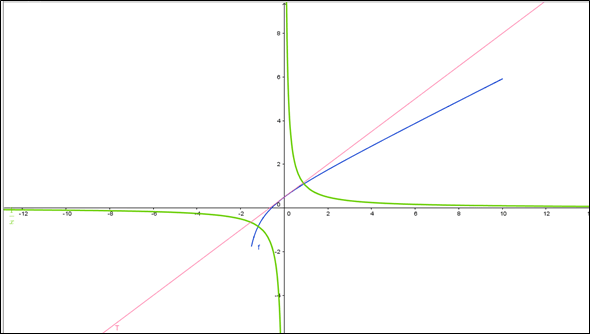
Je détermine graphiquement le nombre de solutions
L’équation f(x) = 1/x admet 2 solutions
Je donne des valeurs approchées
Je mets un quadrillage afin d’avoir une lecture plus affinée (Graphique / Grille)
Pour affiner encore ma lecture, je peux positionner un point sur chaque intersection

Les deux valeurs approchées de la solution de l’équation f(x) = 1/x sont -1,20 et 0,9
7°) En utilisant votre calculatrice et en décrivant les étapes, déterminer une valeur approchée à 10-3 près de la solution positive de l’équation f(x) = 1/x
Avec Géogébra
Calcul formel : Résoudre[ <Équation en x> ] |

AUTRES ARTICLES